funciones trigonometricas 

1. para las funciones de 30º y 60º ; dados un triángulo equilatero ( 3 lados y 3 angulos iguales )en la que se ha trazado una de sus alturas se tiene como longitud  de lado 2 unidades 
2. para un ángulo de 45º estas funciones trigonometricas son determinadas en base a un cuadrado cuya magnitud de lado es 1 unidad y en la que se ha trazado 1 de sus diagonales dividiendo el ángulo recto en dos ángulos de 45º

   oº                                           90º                                       180º                                 270º

sen oº = 0                          sen 90º = 1                            sen 180º =  0                         sen 270º = -1
cos 0º = 1                          cos 90º = 0                            cos 180º = -1                        cos 270º = 0
tg   0º = 0                           tg   90º =  infinito                   tg   180º =  0                          tg   270º = infinito
ctg 0º = infinito                   ctg 90º = 0                            ctg  180º = infinito                  ctg  270º = 0
sec 0º = 1                           sec 90º= infinito                     sec 180º = -1                         sec 270º = infinito
csc 0º = infinito                   csc 90º= 1                             csc 180º = 0                          csc 270º = -1

	sen	cos	tg	ctg	sec	csc
0º	0	1	0	INF	1	INF
90º	1	0	INF	0	INF	1
180º	0	-1	0	INF	-1	INF
270º	-1	0	INF	0	INF	-1
360º	0	1	0	INF	1	INF

MEDIDAS DE ANGULOS

•                      medidas de ángulos en grados

•                      medidas de ángulos en radianes

Medidas de ángulos en grados

En este sistema la unidad de un grado que es el ángulo que subtiende un arco de la  circunferencia igual a 1/360

 MEDIDAS DE ANGULOS EN RADIANES

En este sistema la unidad es el radian que suscribe un arco cuya longitud es igual  a la longitud del radio  

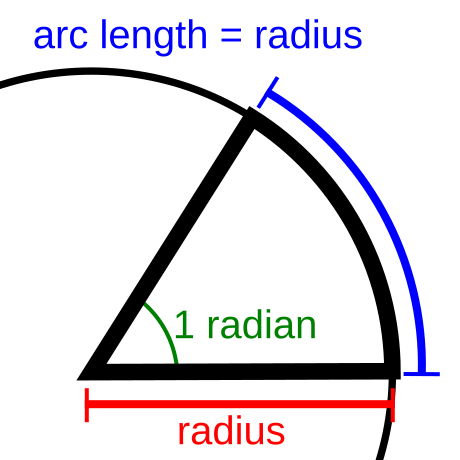
   Transformación  de angulos en grados o en radianes

1 GRADO = π/180º = 0.017453 RAD

1 RADIAN = 180º/π =57,2958º

EJEMPLOS:

• TRANSFORMAR LOS SIGUIENTES ANGULOS DADOS EN MEDIDA CIRCULAR A GRADOS 

π/2=  π/2 . 180/π = 90º                          2π/3 = 2π/3 . 180/π =180º

2π = 2π . 180/π = 360º                          π+1/3= 1.38(57.2958)= 79º 05º 54.95º

• LOS SIGUIENTES ANGULOS ESTAN DADOS EN GRADOS , TRANSFORMARLO A MEDIDA CIRCULAR

150º= 150 . π/180 =  5π/6                      35º 46º 18º = 35.77º (0.017453)= 0.624 RAD

240º = 240 . π/180 = 4π/3

    RESOLUCIÓN DE POLIGONOS REGULARES

Resolución de triángulos isosceles

K

 CIRCUNFERENCIA CIRCUNSCRITA AL POLÍGONO 

1)  α= 360º/n

n= número de lados del polígono

2) α/2= 360/n/2 = 180/n

3) 

                                                                 R

                                                                          C/2

4) Area del triángulo isosceles c.r/2

5) Área del polígono  c.r.n/2

6) Perimetro   c.n

Ejemplo:

RESOLVER EL SIGUIENTE POLIGONO REGULAR

 

DATOS :

r =18

n= 10

1) calculo  α/2 = 180/n=  18                       Área del triángulo                 Área del poligono

2) cos 18º = r/R =18 /R                          A= c.r/2                                    A= C.r.n/2

   R=18/ cos 18 =18.93                           A= 11.69(18)/2                        A=11.69(18)(10)/2 =1052.1 u

   tg 18º  = C/2/r = C/36                          A= 105.21 u                          Perimétro del poligono

  C = 36 tg 18º = 11.69                                                                        c.n= 11.69 * 10= 116.9 u

 TÉRMINOS EMPLEADOS EN PROBLEMAS TRIGONOMÉTRICOS

 

• VERTICAL DE UN LUGAR ._ es  la línea que coincide con la dirección de la plomada 

 

•  LÍNEA HORIZONTAL ._ Es la perpendicular a la vertical 

 

• UN PLANO VERTICAL ._ Es el que contiene a la vertical (pared)

 

• UN PLANO HORIZONTAL._ Es el plano perpendicular a la vertical (piso)

 

• ÁNGULO DE ELEVACIÓN ._ Es el ángulo vertical formado por la visual del observador y la visual del objeto

 

• ÁNGULO DE DEPRESIÓN ._Es el ángulo vertical formado por la visual

APLICACIONES

1) Un navio sale exactamente sobre el rumbo nor -este  ala velocidad de 10 millas por hora . Hallar  la velocidad a la cual se esta moviendo hacia el norte 

 

 V = 10 millas . hora 

sen 45º = vy/v = vy / 10 millas .hora 

Vy = 10 millas . Sen 45º

Vy = 7.07 millas / hora 

 2) Dos boyas son observadas en la dirección sur  desde lo alto de un acantilado cuya parte superior esta a 312 m sobre el nivel del mar ¿ Hallar la distancia entre las dos boyas si sus angulos de depresión medidos desde la punta del acantilado son 46º18º y 27º15º respectivamente .

 

X1= 312/tg                                         X2 = 312/ tg

X1= 312/46.3                                     X2=605.78

X1= 298.15